Breaking Extended Vigenere Cipher
For Appliced cryptography Course for this semester in NYU Tandon, I have been assigned a project to break a vigenere cipher but an extended version. Since I had already done a homework in KAIST, which was to write Kasiski examination program in OCaml, I thought it was going to be a piece of cake. However, the little tweak in the encryption scheme made it a lot more interesting. It was quite painful to come up with other techniques to break the cipher, but knowledges gained the hard way dies hard. And I want to share my thought process!
The cryptanalysis program I had to write has access to information below:
- The ciphertext
- The (partial) knowledge of the encryption scheme
- A set of plaintexts
The extension of Vigenere cipher is that a pseudo-random character can be inserted at a random location in the ciphertext, with a known probability. And other encryption process was exactly the same as the Vigenere cipher. For example, each character in the ciphertext has a 5% chance of being a random character.
Guessing the key length
Guessing a key length in Vigenere cipher is a well-known attack. Kasiski examination and index of coincidence are two of the most famous techniques. Since I had an experience of writing a Kasiski examination program in OCaml, I thought it would be a good idea to try it first. But it turned out that Kasiski examination can’t perform well to this case. The random character extension was enough to make the guess fail.
Similarly, index of coincidence also failed to guess the key length, probably with a similar reason. So I had to come up with another idea.
Chosen plaintext attack
Attacking a key length was inherently difficult because it only uses the ciphertext and the knowledge of the encryption scheme. However, if you look closely to the information you can access, you will find that you can actually use the plaintexts as well.
In modern cipher, having access to plaintexts is not a big deal because the encryption scheme is designed to be secure even if the attacker has access to plaintexts, proven by the computational indistinguishability.
But, in this scheme, the encryption is too weak to be attacked by the chosen plaintext attack. This first thing I tried was to substract the ciphertext by a plaintext. Since it is poly-alphabetic substitution cipher, the result of the substraction will be a key stream. If you get the key, you just decrypt the whole ciphertext, right?
The example below shows the result of substraction of ciphertext by plaintexts.
The repeating 2, 3, 4, 1 cleary shows that that is the key.
C: [4, 4, 22, 14, 11, 8, 23, 21, 2, 11, 5, 20, 22, 8, 23, 1, 21, 19, 5, 5]
P: [2, 1, 18, 13, 9, 5, 19, 20, 0, 8, 1, 19, 20, 5, 19, 0, 19, 16, 1, 4]
D: [2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1]
But this example is more interesting: there is no repeating pattern in the difference. But if you remove the 4-th character (0-based) in the ciphertext, you can see the repeating pattern. We now can tell that is the random character inserted!
C: [6, 8, 18, 22, 11, 16, 6, 13, 2, 22, 12, 13, 19, 15, 2, 6, 12, 19, 17, 14]
P: [4, 5, 14, 21, 14, 3, 9, 1, 20, 9, 15, 14, 0, 3, 8, 18, 15, 14, 1, 24]
D: [2, 3, 4, 1, 24, 13, 24, 12, 9, 13, 24, 26, 19, 12, 21, 15, 24, 5, 16, 17]
Attacking the random characters
Thus, if we are able to tell whether a character is a random character or not, it is now so trivial to decrypt the ciphertext. Then how can we tell that?
I used two methods for the question:
- Information Entropy, and
- Fourier Transform
Information entropy is a measure of the randomness, or the uncertainty of a random variable. The higher the entropy is, the more random the variable is (it gets harder to tell outcome of the next event.) Therefore, if we remove the random characters, the entropy of the ciphertext will decrease.
And Fourier Transform is a method to decompose a signal into its frequency components. Looking at the frequency components of the ciphertext, we can tell whether removing characters reveals a periodic pattern or not. (A key is used repeatedly in Vigenere cipher)
Now we have ideas. And it’s time to demonstrate them!
Test cases
To prove our idea is valid, I needed to test it with some test cases. To generate test cases, I wrote a Python program that generates ciphertexts from a set of plaintexts, with an input key. Surely, it insertes random characters with a given probability.
For keys of length 4~24 (inclusive), I generated 5 ciphertexts for each key length,, since the number of plaintexts in the set is 5. That is, i-th ciphertext of key length k is encrypted from i-th plaintext of the set.
Is entropy a good method?

The plot shows how many cases can be guessed correctly measuring entropy. For each difference (substration of ciphertext to plaintext), I calculated entropy of the difference of the first 30(N) characters. I only calculated ones of the first ones because the characters are likely to be random characters as it is placed at the rear part of the ciphertext.
And for each ciphertext, I measured entropy to each plaintext, and picked the one with the lowest entropy,
if it is significantly lower than the others.
For the significance, I used mean and standard deviation.
A difference whose entropy is lowerthan mean - multiplier * std is considered to be significantly lower.
The multiplier is chosen to be 0.186, because it eliminates all false positive cases.
Just using entropy, we decrypted 16 cases of 105, which was interesting. But it was not enough to decrypt all the cases! The failing cases are due to random characters at the beginning of a ciphertext, because it increases entropies of all the differences derived from the ciphertext.
Then we needed to find a way to eliminate the random characters at the beginning of a ciphertext.
Again, entropy
So, to recover the repeating pattern in the difference, I used again entropy! A simple idea that if a random character is removed entropy will decrease is used here.
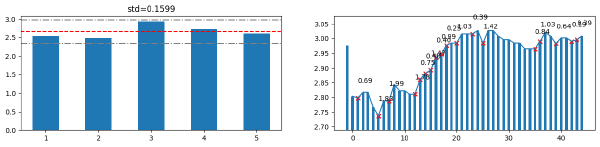
The left plot shows that mere entropy test does not tell anything about the entropy here. (The correct answer is 3, but the entropy of that one is the largest!) But the test fails because we set the multiplier not to accept this result.
The right plot shows how entropy changes if i-th character is removed. We can observe a V-shaped local minimum around the correct answer, which removes 8-th character.
Removing characters at the local minima, we might reveal the hidden repeating pattern. But we need more evidence the numbers are repeating or not.
Fourier Transform
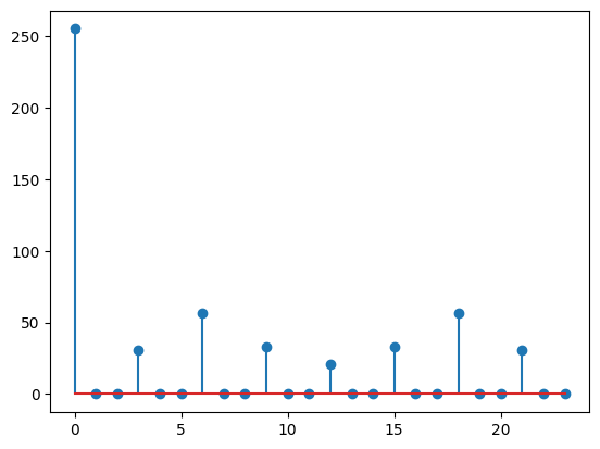
This figure shows magnitudes of Fourier Transform computed on the difference which shows the repeating pattern. You see how many zero-magnitude frequencies are there in the plot? I don’t know how Fourier Transform works, but it was a clear pattern when the difference has a repeating pattern.
Result 1
So the pipeline now looks like this:
- Run entropy test to see if there is a significantly low entropy.
- If not, try removing a character with entropy change and run FFT test.
- If failed to find a repeating pattern, just pick the one with the lowest entropy.
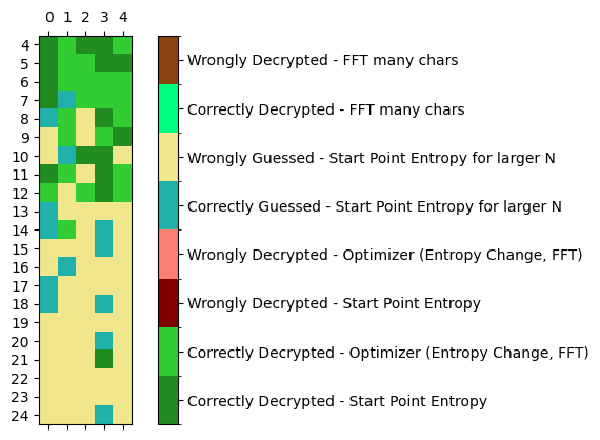
It now correctly decrypts 47.62 percent of all test cases just in 100 miliseconds. Looks good! But, I wanted to go further.
Going further
After looking at failing cases, I found that if there are more than two random characters inserted, the method has no way to decrypt the ciphertext. So I allowed the program to remove 2~4 characters, only if the entropy change is significant.
When I allowed removing 4 characters, the program started to suffer from poor performance. Scrutinizing the algorithm used, I found that computing differences was a performance bottleneck. But I realized from the removed ciphertext and palintexts can be precomputed. Since removing a character shifts all the characters after, the difference can be computed by just removing the first character. The difference contains difference we looking for. Now all we have to do is just taking a slice of it.
So the additional test layer is added to the pipeline:
For the first 48 characters of the ciphertext (which is the minimum length for the repeating pattern to appear even for the longest key length, or 24), run entropy test to ciphertexts with 2~4 characters removed. If there is a significantly low entropy, run FFT test.
Now the result is more satisfactory.

It correctly decrypts 63.81% of all test cases with maximum 17s running time.
Conclusion
I have demonstrated how to break an extended Vigenere cipher with a chosen plaintext attack. The idea was to use entropy and Fourier Transform to find a repeating pattern in the difference of ciphertext and plaintext. The program I wrote correctly decrypts 63.81% of all test cases with maximum 17s running time on my laptop.
I explored the notion of entropy and Fourier Transform, and skills to improve performance of a program by precomputation (nice refresh for performance optimization!)
The full report can be found here: https://docs.google.com/document/d/e/2PACX-1vTomgI21nstUMmi3HSI8N7bbqmHNSCSRXoyfFq23_fWK5_f9VmcmNwj4pe22cFeR562FZ2lhKqt_S-B/pub